This chapter gives an overview over the available algorithms in ViennaCL. The focus of ViennaCL is on iterative solvers, for which generic implementations that allows the use of the same code on the CPU (either using Boost.uBLAS, Eigen, MTL4, or ViennaCL types) and on the GPU (using ViennaCL types) are provided.
ViennaCL provides triangular solvers and LU factorization without pivoting for the solution of dense linear systems. The interface is similar to that of Boost.uBLAS.
In ViennaCL there is no pivoting included in the LU factorization process, hence the computation may break down or yield results with poor accuracy. However, for certain classes of matrices (like diagonal dominant matrices) good results can be obtained without pivoting.
It is also possible to solve for multiple right hand sides:
Iterative solvers approximately solve a (usually sparse) system 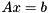 through iterated application of the matrix
through iterated application of the matrix 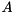 to vectors. ViennaCL provides the following iterative solvers for use with both assembled matrices as well as in a so-called matrix-free setting, where to user provides the operator
to vectors. ViennaCL provides the following iterative solvers for use with both assembled matrices as well as in a so-called matrix-free setting, where to user provides the operator 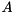 :
:
| Method | Matrix class | ViennaCL |
|---|---|---|
| Conjugate Gradient (CG) | symmetric positive definite | y = solve(A, x, cg_tag()); |
| Mixed-Precision Conjugate Gradient (Mixed-CG) | symmetric positive definite | y = solve(A, x, mixed_precision_cg_tag()); |
| Stabilized Bi-CG (BiCGStab) | non-symmetric | y = solve(A, x, bicgstab_tag()); |
| Generalized Minimum Residual (GMRES) | general | y = solve(A, x, gmres_tag()); |
Linear solver routines in ViennaCL for the computation of 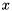 in the expression
in the expression 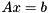 with given
with given 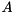 ,
, 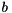 .
.
Pipelined versions of CG, BiCGStab as well as GMRES are implemented for the case that no preconditioner is provided. This provides performance benefits for medium-sized systems of about 10k to 100k unknowns, because kernel launch and data transfer latencies are reduced by a factor of two to three.
Unlike direct solvers, the convergence of iterative solvers relies on certain properties of the system matrix. Keep in mind that an iterative solver may fail to converge, especially if the matrix is ill conditioned or a wrong solver is chosen.
examples/tutorials/ folder.The conjugate gradient method is the method of choice for many symmetric positive definite systems. A minimal snippet for running a CG solver is as follows:
A preconditioner object can be passed as optional fourth argument to the solve() routine. Customized iteration counts as well as relative or absolute tolerances can be provided through the respective member functions of cg_tag: The convention is that solver tags take the relative error tolerance as first argument and the maximum number of iteration steps as second argument. Furthermore, after the solver run the number of iterations and the estimated error can be obtained from the solver tags as follows:
Absolute tolerances can be set via the member function abs_tolerance().
An initial guess 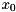 for the iterative solution of the system
for the iterative solution of the system 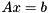 can be incorporated manually by considering
can be incorporated manually by considering
![\[ x = x_0 + y \\ \Rightarrow A(x_0 + y) = b \Leftrightarrow Ay = b - Ax_0 := \tilde{b} \]](form_126.png)
Thus, one may provide a nonzero initial guess by supplying the modified right hand side 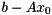 instead of
instead of 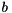 . The obtained solution
. The obtained solution 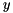 then needs to be added to
then needs to be added to 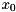 to obtain
to obtain 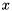 .
.
If a custom monitor callback function should be provided, or ViennaCL should deal with the initial guess internally, then the extended CG interface is required. This extended interface relies on the solver class cg_solver<T>, which takes the vector type as template argument and the cg_tag as constructor argument. A custom monitor callback routine returns a bool and takes the following three parameters:
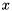
true, the iterative solver terminates. If the monitor returns false, the iterative solver may still terminate because the maximum iteration count, or the absolute or relative tolerance is reached.An exemplary code snippet for a CG solver with custom monitor callback and initial guess is as follows:
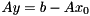 if an initial guess is provided.
if an initial guess is provided.A mixed precision CG solver is available for symmetric positive systems with low to moderate condition number in double precision. The solver operates in a two-stage manner: The residual is computed in double precision, for which a correction is then computed in low precision.
While single precision floating point numbers only require half the number of bytes as double precision floating point numbers, in practice one also needs to transfer indices. This limits the possible performance gains over a conventional CG method to about 20 percent in practice. Also, a mixed precision solver is fairly sensitive with respect to high condition numbers, hence we advise users to only use a mixed precision CG if the system matrix is known to be well-behaved.
Sample code for running a mixed-precision CG solver is as follows:
As usual, the first parameter to the constructor of mixed_precision_cg_tag is the relative tolerance for the residual, while the second parameter denotes the maximum number of solver iterations. The third parameter denotes the relative tolerance for the inner low-precision CG iterations and defaults to 0.01.
examples/banchmarks/solver.cpp for an example.double precision.Currently no extended interface for passing monitors or initial guesses is available for the mixed precision CG solver.
The BiCGStab method is an attractive option for non-symmetric systems. It can be used for general systems, but it is not guaranteed to converge. In comparison to GMRES, BiCGStab has constant costs per iteration and lower memory footprint.
In its shortest form, a BiCGStab solver is called as follows:
Similar to the CG method, relative tolerances and maximum iteration counts can be passed to the constructor of the bicgstab_tag object.
An extended interface for custom monitors and initial guesses is available. The templated class viennacl::linalg::bicgstab_solver<VectorT> is used in exactly the same way as cg_solver above.
ViennaCL provides an implementation of the GMRES method with (optional) restart. GMRES is guaranteed to converge after 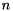 steps for a system with
steps for a system with 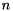 unknowns, even though in practice one usually needs significantly less iterations. The computational cost of GMRES grows with the number of iterations, hence GMRES is either used with a restart after every
unknowns, even though in practice one usually needs significantly less iterations. The computational cost of GMRES grows with the number of iterations, hence GMRES is either used with a restart after every 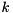 steps, or with a good preconditioner.
steps, or with a good preconditioner.
A sample code snippet for running the GMRES solver in ViennaCL is as follows:
ViennaCL provides (partially) generic implementations of several preconditioners. The preconditioner setup is expect for simple diagonal preconditioners always carried out on the CPU host due to the need for dynamically allocating memory. Thus, one may not obtain an overall performance benefit if too much time is spent on the preconditioner setup.
An overview of preconditioners available for the various sparse matrix types is as follows:
| Matrix Type | ICHOL | (Block-)ILU[0/T] | Jacobi | Row-scaling | AMG | SPAI |
|---|---|---|---|---|---|---|
compressed_matrix | yes | yes | yes | yes | yes | yes |
coordinate_matrix | no | no | yes | yes | no | no |
ell_matrix | no | no | no | no | no | no |
hyb_matrix | no | no | no | no | no | no |
sliced_ell_matrix | no | no | no | no | no | no |
We aim to provide broader support for preconditioners using other sparse matrix formats in future releases. Sparse approximate inverse (SPAI) preconditioners are described in Additional Algorithms section.
Incomplete LU (ILU) factorizations are popular black-box preconditioners and may work in cases where more advanced and problem-specific techniques such as multigrid approaches are not possible. A drawback of classical ILU algorithms is the sequential nature, which prohibits good performance on massively parallel hardware such as GPUs.
ViennaCL provides an implementation of the recently proposed parallel ILU factorization algorithm proposed by Chow and Patel [7]. While the authors propose an asynchronous algorithm, we use a synchronous variant for reasons of better maintainability and user support in the case of failures. Internal evaluations suggest that the performance difference of the synchronous and asynchronous variants are negligible in practice. Also, the static pattern of 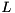 and
and 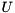 are taken from the system matrix
are taken from the system matrix 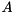 for efficiency reasons.
for efficiency reasons.
The preconditioner exposes two parameters: First, the incomplete factors 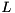 and
and 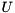 with
with 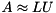 are computed in parallel using a nonlinear iteration scheme. The number of these sweeps can be adjusted in the configuration class
are computed in parallel using a nonlinear iteration scheme. The number of these sweeps can be adjusted in the configuration class chow_patel_tag. Second, the forward- and backward solves in the preconditioner application is approximated by a Jacobi method for the truncated Neumann series. That is, instead of the forward- or backward substition when solving 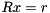 for some vector
for some vector 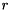 and lower or upper triangular matrix
and lower or upper triangular matrix 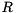 , one or several Jacobi iterations of the form
, one or several Jacobi iterations of the form
![\[ x_{k+1} = (I - R)x_k + D^{-1} b \]](form_133.png)
are used. The number of Jacobi iterations for each triangular factor is a second parameter. For full details of the underlying algorithm we refer to the original paper [7].
The preconditioner class is chow_patel_ilu_precond<MatrixT> with sparse matrix type MatrixT. MatrixT is currently limited to compressed_matrix, which denotes the system matrix type passed as first parameter. A sample code snippet for using the Chow-Patel-ILU0 preconditioner with a BiCGStab solver is as follows:
Even though the setup and solve phase are executed on the GPU when using the CUDA or OpenCL backend, any overall performance gains are highly problem-specific. The number of nonlinear sweeps and Jacobi iterations need to be set problem-specific for best performance. Values between one and four are likely to give best results.
The parallel incomplete Cholesky factorization is similar to the parallel Chow-Patel-ILU0 preconditioner in the previous section, but with a factorization $LL^T$ for symmetric positive definite matrices. The associated preconditioner class is chow_patel_ichol_precond<MatrixT> and used in the same way as the class chow_patel_ilu_precond` described above:
The configuration tag of type chow_patel_tag is of the same type for both the incomplete LU and the incomplete Cholesky factorization case. Thus, the same parameters are exposed for tweaking.
The incomplete LU factorization preconditioner aims at computing sparse matrices lower and upper triangular matrices 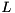 and
and 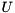 such that the sparse system matrix is approximately given by
such that the sparse system matrix is approximately given by 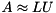 . In order to control the sparsity pattern of
. In order to control the sparsity pattern of 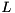 and
and 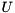 , a threshold strategy is used (ILUT) [26] . Due to the serial nature of the preconditioner, the setup of ILUT is always computed on the CPU using the respective ViennaCL backend.
, a threshold strategy is used (ILUT) [26] . Due to the serial nature of the preconditioner, the setup of ILUT is always computed on the CPU using the respective ViennaCL backend.
The triangular substitutions may be applied in parallel on GPUs by enabling level-scheduling [26] via the member function call use_level_scheduling(true) in the ilut_config object.
Three parameters can be passed to the constructor of ilut_tag: The first specifies the maximum number of entries per row in 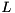 and
and 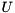 , while the second parameter specifies the drop tolerance. The third parameter is the boolean specifying whether level scheduling should be used.
, while the second parameter specifies the drop tolerance. The third parameter is the boolean specifying whether level scheduling should be used.
Similar to ILUT, ILU0 computes an approximate LU factorization with sparse factors L and U. While ILUT determines the location of nonzero entries on the fly, ILU0 uses the sparsity pattern of A for the sparsity pattern of L and U [26] Due to the serial nature of the preconditioner, the setup of ILU0 is computed on the CPU.
The triangular substitutions may be applied in parallel on GPUs by enabling level-scheduling [26] via the member function call use_level_scheduling(true) in the ilu0_config object.
One parameter can be passed to the constructor of ilu0_tag, being the boolean specifying whether level scheduling should be used.
Similar to the Chow-Patel-family of incomplete LU and incomplete Cholesky factorization preconditioners, ViennaCL also provides a 'classical' incomplete Cholesky factorization preconditioner with static pattern identical to the system matrix. A sample code snippet is as follows:
No level scheduling is currently available for this preconditioner.
To overcome the serial nature of ILUT and ILU0 applied to the full system matrix, a parallel variant is to apply ILU to diagonal blocks of the system matrix. This is accomplished by the block_ilu preconditioner, which takes the system matrix type as first template argument and the respective ILU-tag type as second template argument (either ilut_tag or ilu0_tag). Support for accelerators using CUDA or OpenCL is provided.
A third argument can be passed to the constructor of block_ilu_precond: Either the number of blocks to be used (defaults to 8), or an index vector with fine-grained control over the blocks.
A Jacobi preconditioner is a simple diagonal preconditioner given by the reciprocals of the diagonal entries of the system matrix. Use the preconditioner as follows:
A row scaling preconditioner is a simple diagonal preconditioner given by the reciprocals of the norms of the rows of the system matrix. Use the preconditioner as follows:
The tag viennacl::linalg::row_scaling_tag() can be supplied with a parameter denoting the norm to be used. A value of 1 specifies the 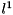 -norm, while a value of
-norm, while a value of 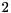 selects the
selects the 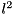 -norm (default).
-norm (default).
Algebraic multigrid (AMG) mimics the behavior of geometric multigrid on the algebraic level and is thus suited for black-box purposes, where only the system matrix and the right hand side vector are available [28] . Many different flavors of the individual multigrid ingredients exist [30], of which some (with an emphasis on fine-grained parallelism) are implemented in ViennaCL.
The two main ingredients of algebraic multigrid are a coarsening algorithm and an interpolation algorithm. The available coarsening methods are:
| Description | ViennaCL option in viennacl::linalg:: |
|---|---|
| One-Pass Classical Coarsening | AMG_COARSENING_METHOD_ONEPASS |
| Sequential Aggregation | AMG_COARSENING_METHOD_AGGREGATION |
| Parallel MIS-2 aggregation (default) | AMG_COARSENING_METHOD_MIS2_AGGREGATION |
AMG coarsening methods available in ViennaCL.
The parallel maximum independent set (MIS) algorithm for distance 2 was initially described in [5] for CUDA. ViennaCL's implementation also supports OpenCL and OpenMP, thus making the method available for all major computing platforms.
The available interpolation methods are:
| Description | ViennaCL option constant |
|---|---|
| Direct interpolation | AMG_INTERPOLATION_METHOD_DIRECT |
| Aggregation | AMG_INTERPOLATION_METHOD_AGGREGATION |
| Smoothed aggregation (default) | AMG_INTERPOLATION_METHOD_SMOOTHED_AGGREGATION |
AMG interpolation methods available in ViennaCL.
The preconditioner setup follows a two-stage process: Parameters for customizing the preconditioner are configured through the viennacl::linalg::amg_tag. Since AMG preconditioners are not a silver bullet, some user customization are typically required for best results. These customizations require a certain familiarity with the concept of multigrid methods. A list of parameters available for tweaks is as follows:
A typical customization code snippet for running the setup on the CPU and the preconditioner application on a CUDA-enabled GPU is as follows:
The actual preconditioner class is viennacl::linalg::amg_precond<MatrixT> for the sparse matrix type MatrixT. Unlike other preconditioner objects, the AMG preconditioner requires an explicit call to the member function .setup() for constructing interpolations, coarse grid hierarchies, etc. A minimal code for using an AMG preconditioner within an iterative solver is as follows:
Two algorithms for the computations of the eigenvalues of a sparse matrix are implemented in ViennaCL:
The algorithms are called for a matrix object A by
Depending on the second parameter tag either of the two methods is called. Both algorithms can be used for either Boost.uBLAS or ViennaCL compressed matrices. In order to get the eigenvalue with the greatest absolut value, the power iteration should be called. The Lanczos algorithm returns a vector of the largest eigenvalues with the same type as the entries of the matrix.
The Power iteration aims at computing the eigenvalues of a matrix by calculating the product of the matrix and a vector for several times, where the resulting vector is used for the next product of the matrix and so on. The computation stops as soon as the norm of the vector changes by less than the prescribed tolerance. The final vector is the eigenvector to the eigenvalue with the greatest absolut value. To call this algorithm, piter_tag must be used. This tag has only one parameter: terminationfactor defines the accuracy of the computation, i.e. if the new norm of the eigenvector changes less than this parameter the computation stops and returns the corresponding eigenvalue (default: 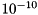 ) The call of the constructor may look as follows:
) The call of the constructor may look as follows:
A minimal example is as follows:
Note that the eigenvalue and eigenvector returned are only approximate. Their accuracy depends strongly on the prescribed tolerance and separation of the largest eigenvalue from the second-largest eigenvalue (both in modulus).
examples/tutorial/power-iter.cppIn order to compute the eigenvalues of a sparse high-dimensional matrix the Lanczos algorithm can be used to find these. This algorithm reformulates the given high-dimensional matrix in a way such that the matrix can be rewritten in a tridiagonal matrix at much lower dimension. The eigenvalues of this tridiagonal matrix are equal to the largest eigenvalues of the original matrix and calculated by using the bisection method [13] . To call this Lanczos algorithm, lanczos_tag must be used. This tag has several parameters that can be passed to the constructor:
factor (default: 0.75)0 uses partial reorthogonalization, 1 full reothogonalization, and 2 does not use reorthogonalization (default: 0)num_eigenvalues (default: 10)krylov_size (default: 100). The maximum number of iterations can be equal or less this parameter.The call of the constructor may look like the following:
examples/tutorial/lanczos.cppA matrix 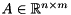 can be factored into
can be factored into 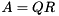 , where
, where 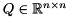 is an orthogonal matrix and
is an orthogonal matrix and 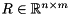 is upper triangular. This so-called QR-factorization is important for eigenvalue computations as well as for the solution of least-squares problems [13] . ViennaCL provides a generic implementation of the QR-factorization using Householder reflections in file
is upper triangular. This so-called QR-factorization is important for eigenvalue computations as well as for the solution of least-squares problems [13] . ViennaCL provides a generic implementation of the QR-factorization using Householder reflections in file viennacl/linalg/qr.hpp. An example application can be found in examples/tutorial/qr.cpp.
The Householder reflectors 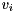 defining the Householder reflection
defining the Householder reflection 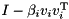 are stored in the columns below the diagonal of the input matrix
are stored in the columns below the diagonal of the input matrix 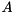 [13] . The normalization coefficients
[13] . The normalization coefficients 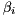 are returned by the worker function
are returned by the worker function inplace_qr. The upper triangular matrix 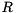 is directly written to the upper triangular part of
is directly written to the upper triangular part of 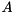 .
.
If 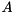 is a dense matrix from Boost.uBLAS, the calculation is carried out on the CPU using a single thread. If
is a dense matrix from Boost.uBLAS, the calculation is carried out on the CPU using a single thread. If 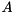 is a
is a viennacl::matrix, a hybrid implementation is used: The panel factorization is carried out using Boost.uBLAS, while expensive BLAS level 3 operations are computed on the OpenCL device using multiple threads.
Typically, the orthogonal matrix 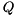 is kept in inplicit form because of computational efficiency. However, if
is kept in inplicit form because of computational efficiency. However, if 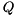 and
and 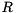 have to be computed explicitly, the function
have to be computed explicitly, the function recoverQ can be used:
Here, A is the inplace QR-factored matrix, betas are the coefficients of the Householder reflectors as returned by inplace_qr, while Q and R are the destination matrices. However, the explicit formation of Q is expensive and is usually avoided. For a number of applications of the QR factorization it is only required to apply Q^T to a vector b. This is accomplished by
without setting up Q (or Q^T) explicitly.
examples/tutorial/least-squares.cpp for a least-squares computation using QR factorizations.